一、时间－空间区域的离散化

首先以一维非稳态导热为例讨论时间－空间的离散化。如图所示。将函数 t 在节点（ n,i+1 ）对点（ n,i ）作泰勒展开，则有： 

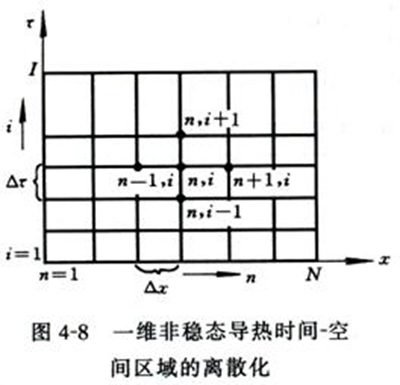
函数 t 在节点（ n,i+1 ）对点（ n,i ）处一阶导数的向前差分公式： 

将函数 t 在节点（ n,i-1 ）对点 (n,i) 作泰勒展开，可得向后差分公式： 

向前差分与向后差分之和，即得中心差分表达式： 

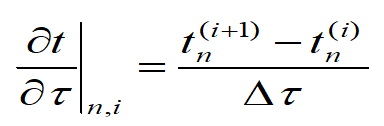
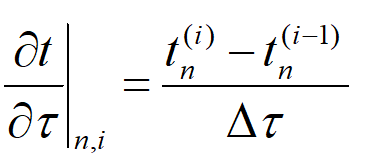
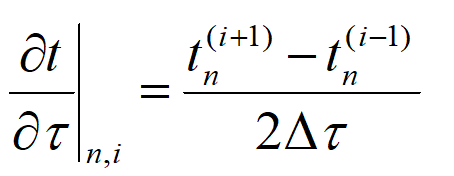
  二、一维平板非稳态导热的显示格式

对一维非稳态方程，扩散项取中心差分，非稳态项取向前差分，则有

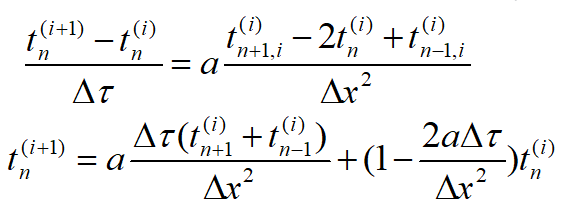
求解非稳态导热微分方程，是从已知的初始温度分布出发，根据边界条件依次求得以后各个时间层上的温度值。由此可见，只要 i 时层上各节点的温度已知，那么 i+1 时层上各节点的温度即可算出，且不需设立方程组求解。此关系式即为显式差分格式。 

优点：计算工作量小； 

缺点：受时间及空间步长的限制。 

三、非稳态导热方程的隐式格式

对一维非稳态导热微分方程中的扩散项在 (i+1) 时层上采用中心差分，非稳态项将 t 在节点（ n,i+1 ）处对节点（ n,i ）采用向前差分，得： 

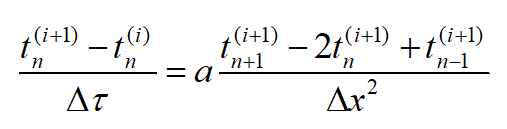
式中已知的是 i 时层上的值，而未知量有 3 个，无法求解，而必须求解（ i+1 ）时层上的一个联立方程组，才能算出 (i+1) 时层各节点的温度，此种差分格式称隐式差分格式。  

优点：不受时间及空间的步长影响； 

缺点：计算工作量大。 

五、一维平板非稳态导热显式格式离散方程组

一维导热显式格式的内节点方程: 

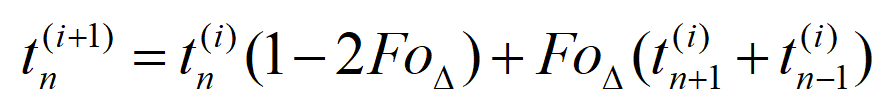
一维导热显示格式的对流边界节点方程： 

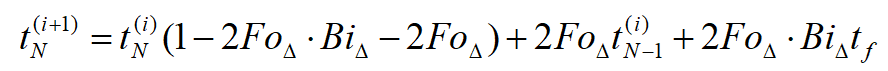
从已知的温度t0出发可以依次求得各时间层的温度值；时间步长和空间步长的选取原则上越小计算结果越精确，但耗时太长，二者之间受到显式格式稳定性的影响。

对于一维导热显式格式的内节点方程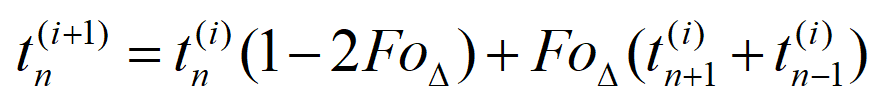 

由方程式得知，点 n 上 i+1 时刻的温度是在该点 i 时刻温度的基础上计及了左右两邻点温度的影响后得出的。若两邻点的影响保持不变，则合理的情况是：i时刻点n的温度越高，则其相继时刻的温度也较高；反之，i时刻点n 的温度越低，其相继时刻的温度也较低。在上式中，满足这种合理性是有条件的，即上式中 前的系数必大于等于零，即 

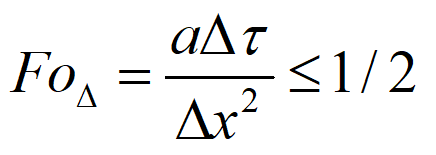
对于一维导热显示格式的对流边界节点方程： 

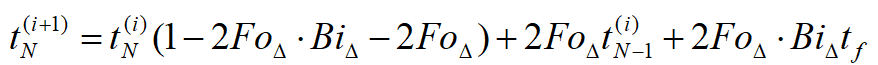
得出合理解的条件是： 

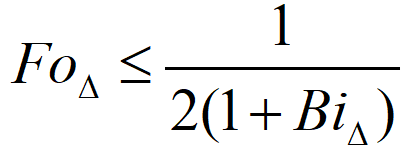
（ 1 ）对流边界节点要得到的合理的解，其限制条件比内节点更为严格，所以，当由边界条件及内节点的稳定性条件得出的网格傅立叶数不同时，应选较小的来确定允许采用的 Δτ。（ 2 ）对于第一、二类边界条件，其限制条件只有内节点的限制条件。 （ 3 ）内、边界节点差分方程的稳定性条件不同，但在数值计算时，二节点又必须选择相同的Δx、Δτ 。因此，在选择了Δx后，则 Δτ的选择就要受到稳定条件的限制，不能任意选择，而必须按两节点的稳定性条件分别计算 ，取其中较小 的作为时间步长，方能满足二者稳定性要求。