对于第一类边界条件的热传导问题，处理比较简单，因为已知边界的温度，可将其以数值的形式加入到内节点的离散方程中，组成封闭的代数方程组，直接求解。

    而对于第二类或第三类边界条件的导热问题，所有内节点的离散方程组成的代数方程组是不封闭的，因未知边界温度，因而应对位于该边界上的节点补充相应的代数方程，才能使方程组封闭，以便求解。

    为了求解方便，这里我们将第二类边界条件及第三类边界条件合并起来考虑，用qw表示边界上的热流密度或热流密度表达式。为使结果更具一般性，假设物体具有内热源 Φ( 不必均匀分布 ) 。

一、边界节点离散方程的建立

1、平直边界上的节点

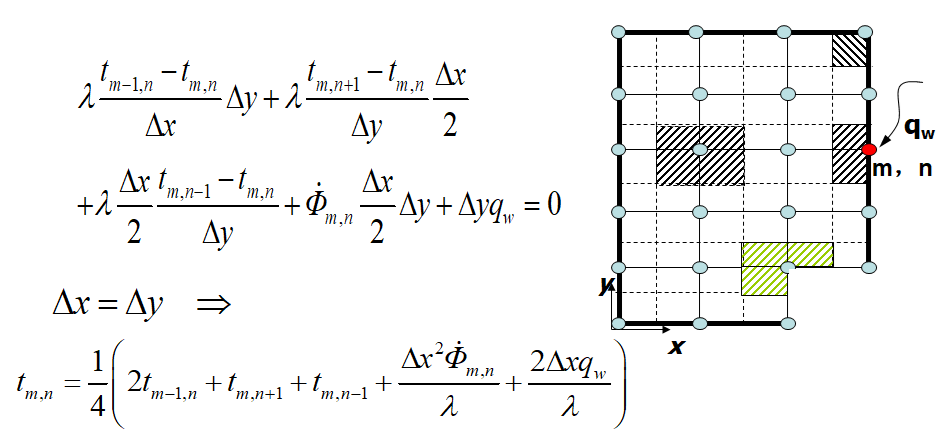
2、外部角点

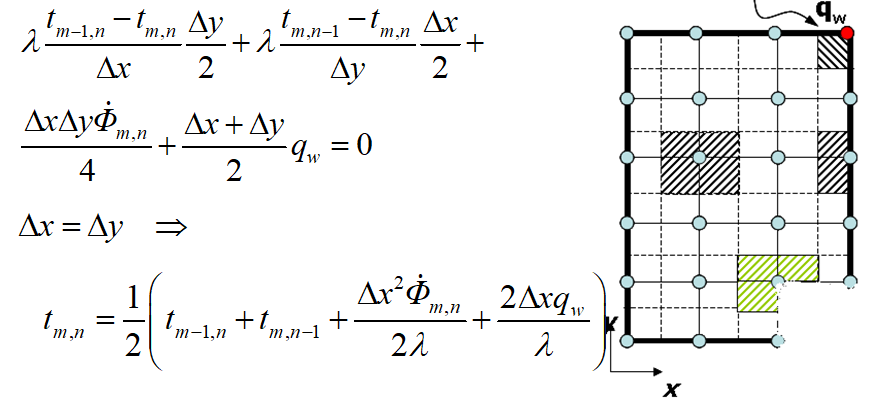
3、内部角点

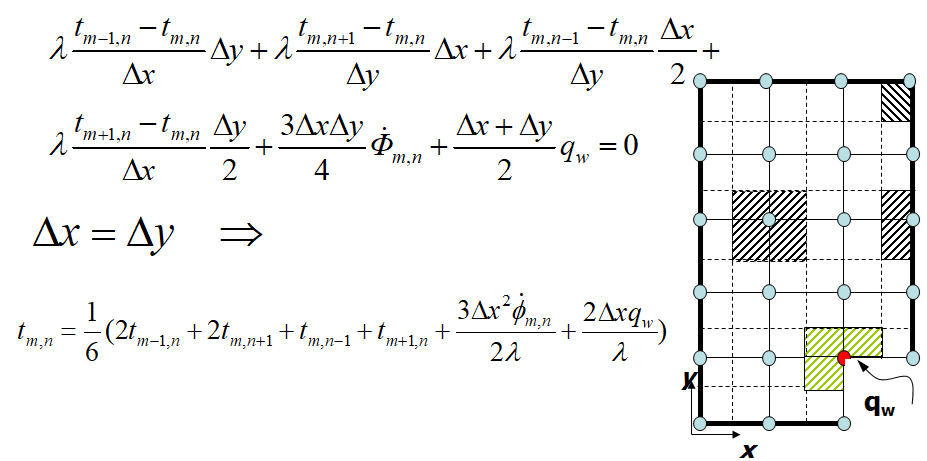
二、求解代数方程的迭代法

1） 直接解法：通过有限次运算获得精确解的方法，如：矩阵求解，高斯消元法。 

2） 迭代法：先对要计算的场作出假设（设定初场），在迭代计算中不断予以改进，直到计算前的假定值与计算结果相差小于允许值为止的方法，称迭代计算收敛。

迭代法目前应用较多的是：1 ）高斯——赛德尔迭代法：每次迭代计算，均是使用节点温度的最新值。 

2 ）用雅可比迭代法：每次迭代计算，均用上一次迭代计算出的值。 

1、高斯——赛德尔迭代法

２、迭代过程是否收敛的判断准则

３、迭代过程能否收敛的判据：

对于一个代数方程组，若选用的迭代方式不合适，有可能导致发散，即称迭代过程发散；对于常物性导热问题组成的差分方程组，迭代公式的选择应使一个迭代变量的系数总是大于或等于该式中其他变量系数绝对值的代数和，此时，结果一定收敛。 采用热平衡法导出差分方程时，若每一个方程都选用导出该方程中心节点的温度作为迭代变量，则上述条件必满足，迭代一定收敛。