一、非稳态导热过程的类型及特点

1、定义

物体的温度随时间而变化的导热过程称非稳态导热。

温度随时间变化，t = f();热流也随时间变化。

２、非稳态导热的分类

周期性非稳态导热：物体的温度随时间作周期性的变化。 

非周期性非稳态导热（瞬态导热）：物体的温度随时间不断地升高（加热过程）或降低（冷却过程），在经历相当长时间后，物体温度逐渐趋近于周围介质温度，最终达到热平衡。物体的温度随时间的推移逐渐趋近于恒定的值。

３、温度分布

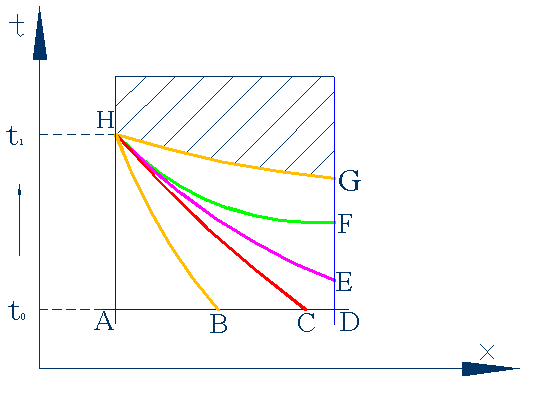
４、两个阶段

非正规状况阶段(右侧面不参与换热，温度分布受初始温度分布的控制 )

正规状况阶段(右侧面参与换热，温度分布受热边界条件的影响 )

５、热量变化

二、导热微分方程解的唯一性定律

(1) 温度分布和热流量分布随时间和空间的变化规律

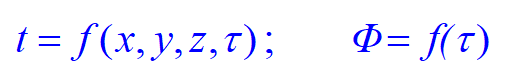
(2) 非稳态导热的导热微分方程式：

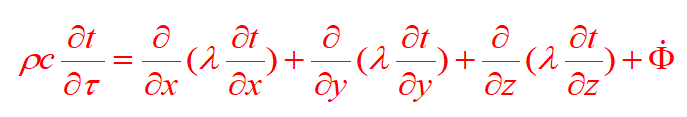
(3) 求解方法：

分析解法：分离变量法、积分变换、拉普拉斯变换

近似分析法： 集中参数法、积分法

数值解法：有限差分法、蒙特卡洛法、有限元法、分子动力学模拟

(4) 解的唯一性

数学上可以证明：某一函数满足上述方程及条件，此函数就是这一特定导热问题的唯一解。即不可能同时存在两个都满足导热微分方程及同一定解条件下的不同的解，称为解的唯一性定律。本章所介绍的分析解都是满足特定问题的唯一解。

三、第三类边界条件下Bi数对平板中温度分布的影响

在第三类边界条件下，确定非稳态导热物体中的温度变化特征与边界条件参数的关系。 

由于平板导热阻力δ/λ与表面对流传热阻力1/h的相对大小不同，平板中温度场会出现三种情形：

由于表面对流换热热阻1/h几乎可以忽略，过程一开始的表面温度就被冷却到t∞。随着时间的推移，平板内部各点的温度逐渐下降而趋近于t∞。

平板内部导热热阻δ/λ几乎可以忽略，任一时刻平板中各点的温度接近均匀，并随着时间的推移整体的下降，逐渐趋近于t∞。

平板中不同时刻的温度分布介于上述两种极端情况之间。

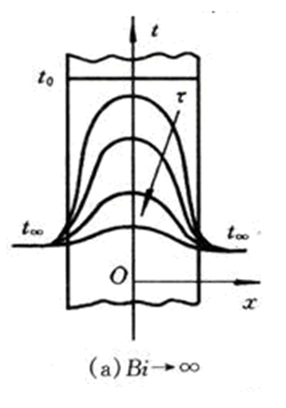
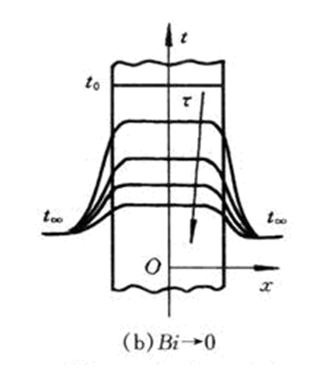
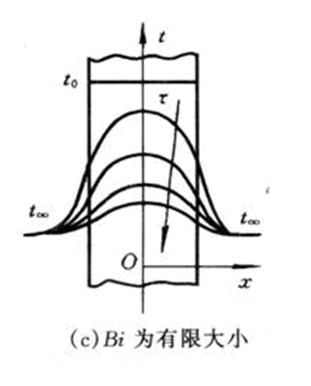
表征这两个热阻比值的无量纲数为毕渥数

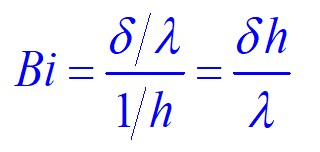
Bi 的大小反映了物体在非稳态条件下内部温度场的分布规律。