前面讲过，热辐射的发射和吸收均具有空间方向特性，因此，表面间的辐射传热与表面几何形状、大小和各表面的相对位置等几个因素均有关系，这种因素常用角系数来考虑。角系数的概念是随着固体表面辐射传热计算的出现与发展，于 20 世纪 20 年代提出的，它有很多名称，如，形状因子、可视因子、交换系数等等。但叫得最多的是角系数。值得注意的是，角系数只对漫射面 ( 既漫辐射又漫发射 ) 、表面的发射辐射和投射辐射均匀的情况下适用。

一. 角系数的定义

定义：把表面1发出的辐射能中落到表面2上的百分数称为表面1对表面2的角系数，记为X1,2。

同理，表面2发出的辐射能中落到表面1上的百分数称为表面2对表面1的角系数，记为X2,1 。                     

假定：（1）所研究的表面是漫射的 

      （2）在所研究表面的不同地点上向外发射的辐射热流密度是均匀的

在这两个假定下，物体的表面温度及发射率的改变只影响该物体向外发射的辐射能的多少而不影响在空间的相对分布，不影响辐射能落到其他表面上的百分数。                                        

  二. 角系数性质

１、角系数的相对性

黑体微元面dA1对微元面dA2的角系数记为Xd1,d2，则根据前面的定义式有

同理，

　　由此可见，

对有限大小表面通过分析可得

以上性质被称为角系数的相对性。

 2、角系数的完整性

 对于有 n 个表面组成的封闭系统，见图9-4所示，据能量守恒可得 :

 上式称为角系数的完整性。若表面 1 为非凹表面时， X 1,1 = 0 。

  3、角系数的可加性

如图 9-5 所示，表面 2 可分为 2a 和 2b 两个面，当然也可以分为 n 个面，则角系数的可加性为

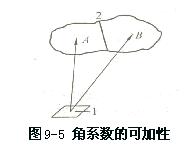
值得注意的是，上图中的表面 2 对表面 1 的角系数不存在上述的可加性。

再来看一下2 对 1 的能量守恒情况:

三．角系数的计算方法

 1、直接积分法

按角系数的基本定义通过求解多重积分而获得角系数的方法

如图所示的两个有限大小的面积，可以得到

2、代数分析法

代数分析法是利用角系数的各种性质，获得一组代数方程，通过求解获得角系数。值得注意的是， (1) 利用该方法的前提是系统一定是封闭的，如果不封闭可以做假想面，令其封闭； (2)凹面的数量必须与不可见表面数相等。下面以三个非凹表面组成的封闭系统为例，如图所示，面积分别为 A1 ， A2 和 A3 ，则根据角系数的相对性和完整性得 :

    通过求解这个封闭的方程组，可得所有角系数，如 X 1,2 为 :

若系统横截面上三个表面的长度分别为l₁，l₂和l₃，则上式可写为

下面考察两个表面的情况，假想面如图9-11所示，根据完整性和上面的公式，有:

解方程组得:

该方法又被称为交叉线法。注意：这里所谓的交叉线和不交叉线都是指虚拟面断面的线，或者说是辅助线