一、管槽内强制对流流动与换热的一些特点

１、两种流态

流体在管道内的流动可以分为层流与湍流两大类，其分界点为以管道直径为特征尺度的Re数，称为临界雷诺数，记为Rec。

２、入口段与充分发展段

流体进入管口后，开始形成边界层，并随流向逐渐增厚。在稳态下，管中心流速将随边界层的增厚而增加，经过一段距离，管壁两侧的边界层将在管中心汇合，厚度等于管半径，同时管断面流速分布和流动状态达到定型，这一段距离通称流动入口段。之后，流态定型，流动达到充分发展，称为流动充分发展段。

热边界层同样存在入口段与充分发展段， 流动入口段与热入口段的长度不一定相等，这取决于Pr，当 Pr ＞1时，流动入口段比热入口段短。 层流时，热入口段长度 L 在常壁温条件下 L/d ≈ 0.05RePr ； 在常热流条件下 L/d ≈ 0.07RePr 。 湍流时L/d<60,一般不区分恒壁温或恒热流边界条件。

在 Pr＝1 情况下，当流动达到充分发展时，换热也进入热充分发展段，无量纲温度分布达到定型，表面传热系数保持不变 。在进口处，边界层最薄，hx具有最高值，随后降低。在层流情况下，hx趋于不变值的距离较长。在紊流情况下，当边界层转变为紊流后，hx将有一些回升，并迅速趋于不变值。

３、两种典型的热边界条件

均匀壁温和均匀热流

湍流：除液态金属外，两种条件的差别可不计

层流：两种边界条件下的换热系数差别明显。

４、流体平均温度以及流体与壁面的平均温差

计算物性的定性温度多为截面上流体的平均温度（或进出口截面平均温度）。在用实验方法测定了同一截面上的速度及温度分布后，采用下式确定该截面上流体的平均温度：

当采用实验方法来测定截面平均温度时，应在测温点之前设法将截面上各部分的流体充分混合。

如果要确定流体与一长通道表面间的平均表面传热系数，在应用牛顿冷却公式时要注意平均温差的确定方法。对恒热流条件，可取       作为   　。

对于恒壁温条件，截面上的局部温差是个变值，应利用  热平衡式：

在分析了管内流体流动传热的一些特征之后，我们就可以对不同流动状态的管内流动传热进行传热计算。这一工作可以在给出相应的准则关系式的基础上进行。

二、管槽内湍流强制对流传热关联式

  1、管内紊流传热准则关系式

    当管内流动的雷诺数 Re ≥ 10 4 时，管内流体处于旺盛的紊流状态。此时的传热计算可采用下面推荐的准则关系式。

（Dittus-Boelter ）准则关系式  

式中， , 可见 特征尺寸为 d ， 特征流速为 u m ，流体物性量采用的定性温度是 ，为流体的平均温度；流体被加热 ，而流体被冷却 。

    公式 6-15 的适用范围是，平直管且管长直径之比; 温差 较小，所谓小温差是指对于气体 , 对于水 ，对于油类流体 ；雷诺数 普朗特数 。

2. 公式的修正 

1 ）温差修正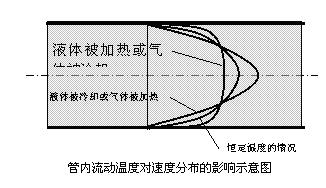

    当流体与管壁之间的温差较大时，因管截面上流体温度变化比较大，流体的物性受温度的影响会发生改变，尤其是流体黏性随温度的变化导致管截面上流体速度的分布也发生改变，进而影响流体与管壁之间的热量传递和交换。流体截面速度分布受温度分布影响的示意图可从右图中观察到。

    因此，在大温差情况下计算传热时准则式右边要乘以物性修正项。对于液体乘以，液体加热 n=0.11 ， 液体冷却 n=0.25 ( 物性量的下标表示在什么温度下取值) ；气体 。

2 ）弯管修正

    如果管子不是平直管，这对流体流动和传热也会产生影响。在弯曲的管道中流动的流体，在弯曲处由于离心力的作用会形成垂直于流动方向的二次流动，从而加强流体的扰动，带来传热的增强。如果管道弯曲的部分比较少，这种影响可以忽略不计。右图显示了弯曲管的流动情况。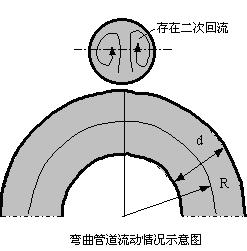弯曲管道内的流体流动传热必须在平直管计算结果的基础上乘以一个大于 1 的修正系数，即 。对于流体为气体时 ; 对于流体为液体时 ；式中 R 为弯曲管的曲率半径。

3 ）入口修正

    当管子的长径比l/d<60 时，属于短管内流动传热，进口段的影响不能忽视。此时亦应在按照长管计算出结果的基础上乘以相应的修正系数，即 。对于尖角入口的短管，推荐的入口效应修正系数为 。

格尼林斯基公式：

三、管槽内层流强制对流传热关联式

管槽内层流充分发展对流传热的理论分析比较成功，有许多代表性的结果可以选用，如书中表６－1至表６－3所示。由表可见：①对于同一截面形状的通道，均匀热流条件下的Nu数总是高于均匀壁温下的Nu数，层流条件下热边界条件的影响不能忽略；②对于等截面直通道，层流充分发展时的Nu数与Re无关；③用当量直径作特征长度，不同截面管道层流充分发展的Nu数也不相等，说明层流时当量直径只是一几何参数不能用来统一不同截面通道的换热与阻力计算的表达式。

实际工程换热设备中，层流时的换热常常处于入口段的范围。可采用下列齐德－泰特公式：

实验验证范围为：

四、微细尺度通道内的流动与传热

气体在微细尺度通道中流动时，气体分子的平均自由程λ与通道的特征尺度l之比称为克努森数，即

根据Kn数大小的不同，可将气体的流动划分为四个区域：

前面介绍的动量方程和能量方程及无速度滑移、无温度跳跃边界条件仅适用于Kn<0.001的连续介质区；在速度滑移和温度跳跃区方程仍适用，但必须采用速度滑移和温度跳跃的条件；在过渡区与自由分子区不再适用，对流动与传热的数学描述需采用基于分子动理论的有关原理与方程。

在微细尺度通道中的流动和传热过程与常规尺度通道中的过程相比有以下特点：

（１）控制过程的作用力会发生变化；

（２）表面粗糙程度的影响更为突出；

（３）通道固壁的导热影响更为明显；

（４）可压缩性会产生重要的影响；

（５）气体稀薄性的影响必须考虑。

纳米流体是指在基础流体中悬浮有许多纳米尺度颗粒的复合流体。当纳米颗粒材料的导热系数大于基础流体时，大量纳米颗粒的存在不仅增加了流体的热容量与表面积，而且大大增加了流体的有效导热系数，有利于强化对流传热。