一、边界层的概念
边界层的概念是1914年普朗特提出的。他认为对流传热热阻的大小主要取决于靠近壁面附近流体的状况,因为粘滞性起作用的区域仅仅局限在靠近壁面的薄层内。在此薄层以内, u、t变化最为剧烈。为计算的简化,因此引入了速度边界层和温度边界层的概念。
1. 速度边界层
1)定义:
流体流过固体壁面时,由于壁面层流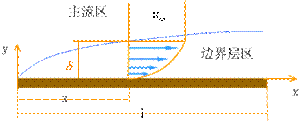 体分子的不滑移特性,在流体黏性力的作用下,近壁流体流速在垂直于壁面的方向上会从壁面处的零速度逐步变化到来流速度,如图5-10所示。流体流速变化的剧烈程度,即该方向上的速度梯度,与流体的黏性力和速度的大小密切相关。普朗特通过观察发现,对于低黏度的流体,如水和空气等,在以较大的流速流过固体壁面时,在壁面上流体速度发生显著变化的流体层是非常薄的。因而他把在垂直于壁面的方向上流体流速发生显著变化的流体薄层定义为速度边界层,而把边界层外流体速度变化比较小的流体流场视为主流区(势流流动区域)。这样,引入边界层的概念之后,流体流过固体壁面的流场就人为地分成两个不同的区域,其一是边界层流动区,这里流体的黏性力与流体的惯性力共同作用,引起流体速度发生显著变化;其二是主流区(势流区),这里流体黏性力的作用非常微弱,可视为无黏性的理想流体流动,也就是势流流动。
体分子的不滑移特性,在流体黏性力的作用下,近壁流体流速在垂直于壁面的方向上会从壁面处的零速度逐步变化到来流速度,如图5-10所示。流体流速变化的剧烈程度,即该方向上的速度梯度,与流体的黏性力和速度的大小密切相关。普朗特通过观察发现,对于低黏度的流体,如水和空气等,在以较大的流速流过固体壁面时,在壁面上流体速度发生显著变化的流体层是非常薄的。因而他把在垂直于壁面的方向上流体流速发生显著变化的流体薄层定义为速度边界层,而把边界层外流体速度变化比较小的流体流场视为主流区(势流流动区域)。这样,引入边界层的概念之后,流体流过固体壁面的流场就人为地分成两个不同的区域,其一是边界层流动区,这里流体的黏性力与流体的惯性力共同作用,引起流体速度发生显著变化;其二是主流区(势流区),这里流体黏性力的作用非常微弱,可视为无黏性的理想流体流动,也就是势流流动。
2)边界层的厚度
我们说边界层是壁面上方流速发生显著变化的薄层,但其边缘所在的位置人们却是模糊的。在实际分析边界层问题时通常规定,当速度变化达到主流速度的99%处的空间位置y为速度边界层的外边缘,那么从这一点到壁面的距离就是边界层的厚度![]() 。
。
3)引入的意义:
a)缩小计算区域。以温度为20℃的空气沿平板的流动为例,在不同来流速度![]() 下,相对于平板长度l,
下,相对于平板长度l,![]() 是一个比l小一个数量级以上的小量。在这样小的薄层内,流体的速度要从0 m/s变化到接近于主流流速,所以流体在垂直于主流方向上的速度变化是十分剧烈的。由于边界层内
是一个比l小一个数量级以上的小量。在这样小的薄层内,流体的速度要从0 m/s变化到接近于主流流速,所以流体在垂直于主流方向上的速度变化是十分剧烈的。由于边界层内![]() 都很大,动量微分方程式中的粘性力和惯性力及能量微分方程中的导热和对流项都需考虑,有了边界层,可以将对流传热的研究集中在边界层内。
都很大,动量微分方程式中的粘性力和惯性力及能量微分方程中的导热和对流项都需考虑,有了边界层,可以将对流传热的研究集中在边界层内。
b)边界层内的流动和传热可以利用边界层的特点进行简化,即在边界层中可以运用数量级的分析方法对纳维-斯托克斯方程进行简化。
例如:运用数量级分析的方法,边界层内粘性流体的稳态动量方程可简化为:
![]()
与二维稳态的纳维—斯托克斯方程相比,上述运动微分方程的特点是:
(i)在u方程中略去了主流方向的二阶导数项;(ii)略去了关于速度![]() 的动量方程。(iii)认为边界层中
的动量方程。(iii)认为边界层中![]() 。
。
4)临界雷诺数:
流体的流动可区别为层流和湍流两种。
 边界层也呈现出层流和湍流。流体以
边界层也呈现出层流和湍流。流体以![]() 的流速沿平板流动。在平扳的起始段,
的流速沿平板流动。在平扳的起始段,![]() 很薄。随着x的增加,由于壁面粘滞力的影响逐渐向内部传递,
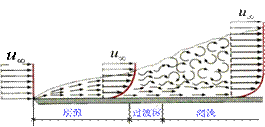
很薄。随着x的增加,由于壁面粘滞力的影响逐渐向内部传递,![]() 逐渐增厚,同时黏性力对流 场的控制作用也逐步减弱,从而使边界层内的流动变得紊乱。在某一距离xc以前一直保持层流特征。此时流体作有秩序的分层运动,各层之间互不干扰。这时的边界层称层流边界层。随着边界层厚度的增加,本来很平顺的层流流动状态就会变成紊乱无序的紊流流动状态。此时流体质点在沿x方向流动的同时,又作着紊乱的不规则脉动,紊流流动状态的边界层则为紊流边界层,我们把边界层从层流过渡到紊流的x值称为临界值,记为xc,其所对应的雷诺数称为临界雷诺数,即Rec。
逐渐增厚,同时黏性力对流 场的控制作用也逐步减弱,从而使边界层内的流动变得紊乱。在某一距离xc以前一直保持层流特征。此时流体作有秩序的分层运动,各层之间互不干扰。这时的边界层称层流边界层。随着边界层厚度的增加,本来很平顺的层流流动状态就会变成紊乱无序的紊流流动状态。此时流体质点在沿x方向流动的同时,又作着紊乱的不规则脉动,紊流流动状态的边界层则为紊流边界层,我们把边界层从层流过渡到紊流的x值称为临界值,记为xc,其所对应的雷诺数称为临界雷诺数,即Rec。
实验研究的数据表明,流体平行流过平板的临界雷诺数大约是(一般对平板:Rec=500000)。当然,这一数据与来流速度的紊流程度和平板前沿的几何形状密切相关,因而临界雷诺数的数值会在一定范围内变动。
我们不难发现,要使边界层的厚度远小于流动方向上的尺度(即l),也就是所说的边界层是一个薄层,这就要求雷诺数必须足够的大。因此,对于流体流过平板,满足边界层假设的条件就是雷诺数足够大。由此也就知道,当速度很小、黏性很大时或在平板的前沿,边界层是难以满足薄层性条件。
4)边界层理论的四个基本要点
a. 当粘性流体沿固体表面流动时,流场划为主流区(势流区)和边界层区。在边界层区内,速度在垂直于壁面方向剧烈变化。而主流区速度低度几乎为零。速度边界层成立的条件是Re>>1。
b. 主流区的流动视为理想流体的流动,用描述理想流体的方程求解。边界层区应考虑粘性的影响,用粘性流体的边界层微分方程求解,其特点是主流方向流速的二阶导数项忽略不计。
c. 边界层的流动状态分为层流和紊流。紊流边界层分为层流底层、缓冲层和紊流核心区。
d.边界层的厚度是与壁面尺寸相比很小的量,且远不只小于一个数量级。即:![]() 。
。
2. 热(温度)边界层
1)定义
当流体流过平板而平板的温度tw与来流流体的温度t∞不相等时(即存在温度差),对于上述的低黏性流体,如果流体的热扩散系数也很小,在壁面上方也能形成温度发生显著变化的薄层,常称为热边界层。
2)热边界层厚度
仿照速度边界层的约定规则,以过余温度为来流过余温度的99%处定义为热边界层的外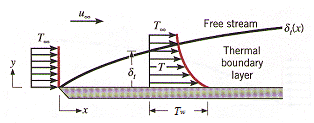 边缘。(当壁面与流体之间的温差达到壁面与来流流体之间的温差的0.99倍时,即,此位置就是边界层的外边缘),而该点到壁面之间的距离则是热边界层的厚度,记为δt 。如果整个平板都保持温度tw,那么,x=0时δt(x)=0,且随着x值的增大逐步增厚。在同一位置上热边界层厚度与速度边界层厚度的相对大小与流体的普朗特数Pr有关,也就是与流体的热扩散特性和动量扩散特性的相对大小有关。理论上
边缘。(当壁面与流体之间的温差达到壁面与来流流体之间的温差的0.99倍时,即,此位置就是边界层的外边缘),而该点到壁面之间的距离则是热边界层的厚度,记为δt 。如果整个平板都保持温度tw,那么,x=0时δt(x)=0,且随着x值的增大逐步增厚。在同一位置上热边界层厚度与速度边界层厚度的相对大小与流体的普朗特数Pr有关,也就是与流体的热扩散特性和动量扩散特性的相对大小有关。理论上
![]()
δt~f(Re×, Pr)
由此式可以看出,热边界层是否满足薄层性的条件,除了Re×足够大之外还取决于普朗特数的大小,当普朗特数非常小时,热边界层相对于速度边界层就很厚,反之则很薄。
二、边界层微分方程组
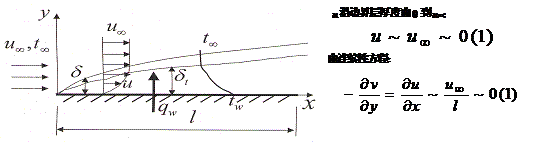
利用上述的边界层的概念,我们可以对流体流过平板的对流传热微分方程组进行相应的简化。按照普朗特的边界层为一个薄层的假设,以及满足这一假设下的流场特征,我们运用数量级分析的方法可以对上述微分方程组在边界层中得以简化。
数量级分析:比较方程中各量或各项的量级的相对大小;保留量级较大的量或项;舍去那些量级小的项,方程大大简化
由边界层假设,如果设定X的数量级为1,(x 与 l 相当),那么Y的数量级定义为Δ(一个小量);在设定主流方向上的速度u 的数量级为1,温度: ![]() 的情况下,对动量微分方程进行数量级分析。
的情况下,对动量微分方程进行数量级分析。
对于稳态过程而言,如不考虑体积力,则动量方程为:
![]()
![]()
分析:因为![]() ,则
,则![]() ~1,
~1,![]() ~
~![]() ;来流速度
;来流速度![]() ~1
~1
(1)比较![]() 与
与![]() :
:
若![]() 的数量级为
的数量级为![]() 即1时,则
即1时,则![]() 的数量级为
的数量级为![]() ,相应地
,相应地![]() ~
~![]() ,而
,而![]() ~1
~1
(2)分析流体垂直于板面方向的速度v相当于什么数量级?
即![]() 必与
必与![]() 属于同一数量级,
属于同一数量级,![]() ~1可以得出v的数量级为Δ。在边界层这样一个极薄的薄层中,流体的垂直速度从平板表面处的零,增加到边界层外缘处的
~1可以得出v的数量级为Δ。在边界层这样一个极薄的薄层中,流体的垂直速度从平板表面处的零,增加到边界层外缘处的![]() ,而其变化率
,而其变化率![]() 的数量级却仍与
的数量级却仍与![]() 相同,这就表明速度v的数值一定大大地低于u的数值,即v~Δ。这样v在x方向上的变化率也必远远小于u在x方向上的变化率,既然
相同,这就表明速度v的数值一定大大地低于u的数值,即v~Δ。这样v在x方向上的变化率也必远远小于u在x方向上的变化率,既然![]() ~1,则
~1,则![]() ~Δ。同理,既然
~Δ。同理,既然![]() ~1,
~1,![]() ~Δ。同(1)分析,
~Δ。同(1)分析,![]() 也必更加大大地大于
也必更加大大地大于![]() ,既然
,既然![]() ~Δ,则
~Δ,则![]() ~
~![]() 。
。
综上所述,动量方程的数量级可分别表示成:
![]() a
a
1 ![]() Δ
Δ ![]()
![]()
![]()
![]() b
b
1 ![]() Δ
Δ ![]()
![]()
![]()
上两式右边括号内的两项相比,后一项要比前一项大得多,所以![]() 和
和![]() 均可略去。在边界层内,粘性力与其它力属于同一数量级,从上两式左边可以看出,惯性力分别相当于1和Δ数量级,按照方程两边数量级应该一致的原则,因此粘性力也必相应地相当于1和Δ数量级,即运动粘度
均可略去。在边界层内,粘性力与其它力属于同一数量级,从上两式左边可以看出,惯性力分别相当于1和Δ数量级,按照方程两边数量级应该一致的原则,因此粘性力也必相应地相当于1和Δ数量级,即运动粘度![]() ~Δ2。
~Δ2。
(3)考察压力梯度的数量级:
在a式中惯性力和粘性力都相当于1的数量级,假定![]() 的数量级是1,那么
的数量级是1,那么![]() 的数量级至多也是1,否则方程式无法成立。同理,
的数量级至多也是1,否则方程式无法成立。同理,![]() 的数量级至多也是Δ,(注意:
的数量级至多也是Δ,(注意:![]() 与
与![]() 不同,紧贴固体表面的流体流速u等于零,但此处的压力并不等于零。边界层断面上的压力变化并非从零变到边界层外的压力p,因而
不同,紧贴固体表面的流体流速u等于零,但此处的压力并不等于零。边界层断面上的压力变化并非从零变到边界层外的压力p,因而![]() ~
~![]() ,但
,但![]() 的数量级却至多只是Δ。)这一结果告我们在边界层中压力不随Y的变化而变化,仅仅是X的函数。
的数量级却至多只是Δ。)这一结果告我们在边界层中压力不随Y的变化而变化,仅仅是X的函数。
(4)比较a式和b式的数量级后,发现b式的各项要比式a的各项小一个数量级,因而b时可以舍去,于是边界层的动量微分方程就由两个变为一个,即 ![]()
而边界层内的压力梯度仅沿 x 方向变化,而边界层内法向的压力梯度极小。即边界层内任一截面压力与 y无关而等于主流压力,则![]()
![]()
当流体纵掠平板时,边界层外主流中的流速没有变化,按照铂努力方程,主流中的压力也不变,![]()
可以得出: ![]()
同样对边界层中二维稳态能量方程进行数量级比较,有
![]()
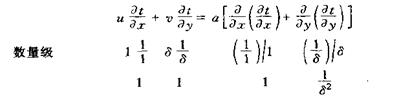

![]()
至此,二维、稳态、无内热源的边界层传热微分方程组为:
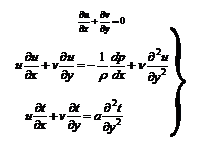
微分方程组经过在边界层中简化后,由于动量方程和能量方程分别略去了主流方向上的动量扩散项和热量扩散项 ,从而构成上游影响下游而下游不影响上游的物理特征。这就使得动量方程和能量方程变成了抛物型的非线性微分方程;且由于动量方程由两个变成为一个,而且项可在边界层的外边缘上利用伯努利方程变成的形式。
于是方程组在给定的边值条件下可以进行分析求解。布劳修斯在引入相似变量下把动量方程变成常微分方程后由进行了求解,而普尔豪森也对能量方程进行了相同的处理。获得相应的速度分布和温度分布,进而求得壁面的摩擦系数和对流传热系数。
普朗特从他多年从事水力学试验中所观察到的事实出发,创造性的用数量级对比法简化了原始的微分方程组,开拓了对流传热理论界的道路,成为流体力学和传热学发展史的里程碑。在他发表边界层微分方程组时,许多著名数学家都不以为然,认为他的这种舍弃微分方程中若干项以至整个方程的做法是荒谬的。(1904年发表)直到1908年,他的学生布劳修斯用边界层方程获得了外掠平板的解,并且其正确性被尔后的实验证实,普朗特的边界层理论才站住脚。所以实验研究仍是技术发展必不可少的。
三、速度边界层厚度与热边界层厚的关系
1.比较边界层的动量方程和能量方程,


动粘性反映了流体中由于分子运动而扩散动量的能力。
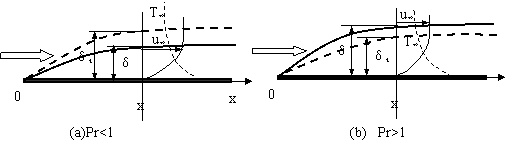
在忽略动量方程压力项后,当Pr=1时,动量方程与能量方程完全相同。即速度分布的解与温度分布完全相同,此时速度边界层厚度等于温度边界层厚度。
当Pr>1时,Pr=υ/a,υ>a,粘性扩散 >热量扩散,速度边界层厚度>温度边界层厚度。
当Pr<1时,Pr=υ/a,υ<a,粘性扩散 <热量扩散,速度边界层厚度<温度边界层厚度。
这也可以从公式得出。