一、通过平壁的导热

平壁的长度和宽度都远大于其厚度，因而平板两侧保持均匀边界条件的稳态导热就可以归纳为一维稳态导热问题。

  　平板可分为单层壁，多层壁和复合壁等类型 。

1 、单层平壁

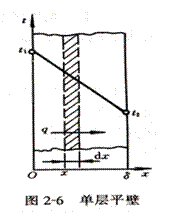
已知：单层平壁两侧恒温且为 t_１、t ₂ , 壁厚 δ，如图2-6 所示，建立坐标系，边界条件为： x=0 时 t=t ₁ ； x=δ 时t=t 2 。温度只在x 方向变化属一维温度场。

    试求：温度分布并确定 q ＝f （  t ₁ ， t ₂ ， λ ， δ ）。

1 ）温度分布

    当 λ ＝const 时，无内热源的一维稳态导热微分方程：

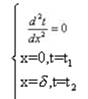
    对此方程积分求其通解（连续积分两次）：

                  t=c ₁x+c ₂

    其中 c ₁ 、 c ₂ 为常数，并且由边界条件确定

    当 x=0 时t=t ₁ ∴ c ₂ = t ₁

    当 x=δ 时 t=t ₂ ∴ c ₁ =(t ₂－t ₁ )/δ

    ∴该条件下其温度分布为：

    又∵ δ 、t ₁ 、 、t ₂ 均属定值　　

    ∴温度成线性关系，即温度分布曲线的斜率是常数（温度梯度）        

2 ）热流密度 q

    把温度分布 dt/dx 代入傅立叶定律 q= -λ(dt/dx) 得；             

若表面积为A, 在此条件下 , 通过平壁的导热热流量则为 :                     此两式是通过平壁导热的计算公式，它们揭示了 q 、 Ф 与 λ 、 δ 和 Δt 之间的关系

2 、热阻的含义

热量传递是自然界的一种转换过程 , 与自然界的其他转换过程类同，如：电量的转换，动量、质量等的转换。其共同规律可表示为： 过程中的转换量 = 过程中的动力 / 过程中的阻力。

由前可知：1） 在平板导热中 导热热流量：，即        (2-1)          

2）在一个传热过程中，根据传热方程式 ，得    (2-2)          

综上比较可见：(2-1) 式中 Ф-------- 热流量为导热过程的转移量；Δ t- ------ 温度为导热过程的动力；   δ/(Aλ) ---- 为导热过程的阻力

(2-2)式中 Ф-------- 传热过程中的热流量为传热过程的转移量；Δ t- ------ 温压为传热过程的动力；------- 传热过程的阻力

    由此引出热阻的概念：

1 ）热阻定义：热转移过程的阻力称为热阻。

2 ）热阻分类：不同的热量转移有不同的热阻，其分类较多，如：导热阻、辐射热阻、对流热阻等。对平板导热而言又分：

    面积热阻 R A ：单位面积的导热热阻称面积热阻。

    热阻 R ：整个平板导热热阻称热阻。　

3 ）热阻的特点：

   串联热阻叠加原则：在一个串联的热量传递过程中，若通过各串联环节的热流量相同，则串联过程的总热阻等于各串联环节的分热阻之和。

因此，稳态传热过程热阻的组成是由各个构成环节的热阻组成，且符合热阻叠加原则。

3 、复合壁的导热情况

    复合壁（多层壁）：就是由几层不同材料叠加在一起组成的复合壁。

    以下讨论三层复合壁的导热问题，如图 2-7 所示：

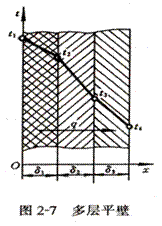    假设条件：层与层间接触良好，没有引起附加热阻（亦称为接触热阻）也就是说通过层间分界面时不会发生温度降。

已知各层材料厚度为 δ₁、 δ₂、 δ₃ 的导热系数为 λ₁ 、λ₂、λ₃ ， 多层壁内外表面温度为 t ₁、t ₄ ， 其中间温度t ₂ 、 t ₃ 未知， λ ＝const 。

试求：通过多层壁的热流密度 q

解：根据平壁导热公式可知各层热阻为

   δ ₁ /λ ₁ =(t₁ -t ₂ )/ q ；δ ₂ /λ ₂ =(t₂ -t ₃ )/ q  ；δ ₃ /λ ₃ =(t₃-t ₄ )/ q

    根据串联热阻叠加原理得多层壁的总热阻为（适用条件：无内热源，一维稳态导热）

     (t ₁ -t₄ )/q=δ ₁ /λ ₁ +δ ₂ /λ ₂ +δ ₃ /λ ₃

则多层壁热流密度计算公式

 q=(t ₁－t ₄ )/ [ δ₁ /λ₁ +δ₂ /λ₂ +δ₃ /λ₃ ]

    将 q 代入各层热阻公式，得层间分界面上未知温度 t ₂；t ₃

    t ₂ = t ₁－q (δ₁ /λ₁ ) ；   t ₃ = t ₂ －q (δ₂ /λ₂ )

    说明：当导热系数 λ 对温度t 有依变关系时，即 λ 是 t 的线性函数时 λ ＝ λ₀ (1+bt)时，只需求得该区域平均温度下的 λ 值，代入以上公式（ λ ＝ const ）即可求出正确结果。

二、通过圆筒壁的导热

1、单层圆筒壁

圆筒壁就是圆管的壁面。当管子的壁面相对于管长而言非常小，且管子的内外壁面又保持均匀的温度时，通过管壁的导热就是圆柱坐标系上的一维导热问题。即一维、稳态、无内热源、常物性的问题。

2、多层圆筒壁

带有保温层的热力管道、嵌套的金属管道和结垢、积灰的输送管道等可看成由不同材料同心紧密结合而构成的多层圆筒壁，如果管子的壁厚远小于管子的长度，且管壁内外边界条件均匀一致，那么在管子的径向方向构成一维稳态导热问题。 

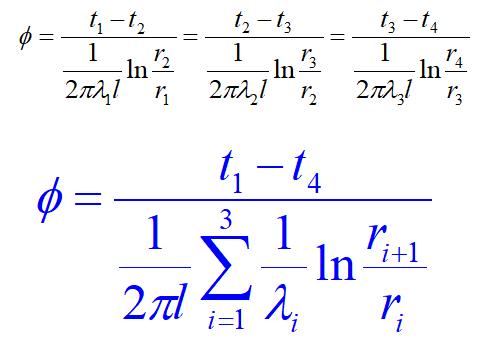
三、通过球壳的导热

对于内、外表面维持均匀恒定温度的空心球壁的导热，在球坐标系中也是一个一维导热问题。相应计算公式为：

               温度分布：                                       热流量：                 热阻：

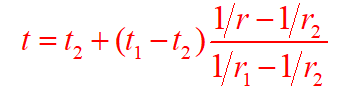
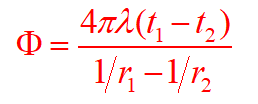
四、带第二类、第三类边界条件的一维稳态导热

一个电熨斗，电功率为1200W，底面竖直置于环境温度为25度的房间中，金属底板厚为5毫米，导热系数为15w/mK，面积为300平方厘米。考虑辐射作用在内的表面传热系数为80W/m2K，试确定稳态条件下底板两表面的温度。

五、变截面或变导热系数的一维问题

求解导热问题的主要途径分两步：

求解导热微分方程，获得温度场；

根据Fourier定律和已获得的温度场计算热流量；

对于稳态、无内热源、第一类边界条件下的一维导热问题，可以不通过温度场而直接获得热流量。对于导热系数为变数或导热面积沿热流密度矢量方向改变的情形特别有效。

分离变量后积分，并注意到热流量Φ与x无关(稳态)，得

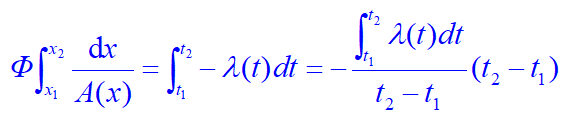
实际上，不论如何变化，只要能计算出平均导热系数，就可以利用前面讲过的所有定导热系数公式，只是需要将换成平均导热系数。