由前可知：
（ 1 ）对于一维导热问题，根据傅立叶定律积分，可获得用两侧温差表示的导热量。
（ 2 ）对于多维导热问题，首先获得温度场的分布函数 
，然后根据傅立叶定律求得空间各点的热流密度矢量。
一 、导热微分方程
1 、定义：根据能量守恒定律与傅立叶定律，建立导热物体中的温度场应满足的数学表达式，称为导热微分方程。
2 、导热微分方程的数学表达式（导热微分方程的推导方法，假定导热物体是各向同性的。）
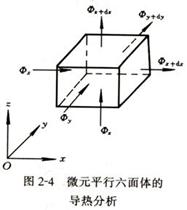
1 ）针对笛卡儿坐标系中微元平行六面体
由前可知，空间任一点的热流密度矢量可以分解为三个坐标方向的矢量。
同理，通过空间任一点任一方向的热流量也可分解为x 、 y 、 z 坐标方向的分热流量，如图2-4 所示。
① 通过 x=x 、 y=y 、 z=z三个微元表面而导入微元体的热流量：фx 、фy 、фz 的计算。
根据傅立叶定律得
（ a ）
② 通过 x=x+dx 、 y=y+dy 、 z=z+dz 三个微元表面而导出微元体的热流量фx+dx 、фy+dy 、фz+dz 的计算。
根据傅立叶定律得：
（b）
③ 对于任一微元体根据能量守恒定律，在任一时间间隔内有以下热平衡关系：
导入微元体的总热流量+微元体内热源的生成热
=导出微元体的总热流量+微元体热力学能（内能）的增量 (c)
其中 微元体内能的增量 =
(d)
微元体内热源生成热 = 
(e)
其中 
、 c 、 
、 
—— 微元体的密度、比热容、单位时间内单位体积内热源的生成热及时间
导入微元体的总热流量фλ = ф x+ ф y+ ф z (f)
导出微元体的总热流量 
(g)
将以上各式代入热平衡关系式，并整理得：
这是笛卡尔坐标系中三维非稳态导热微分方程的一般表达式。
其物理意义：反映了物体的温度随时间和空间的变化关系。
讨论：
① 
时
其中a = 
——称扩散系数（热扩散率）
② 物体内无内热源，即 
=0
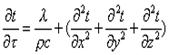
③ 若 时，且属稳态，即： 
=0
即数学上的泊松方程。该微分方程属常物性、稳态、三维、有内热源问题的温度场控制方程式。
④ 常物性、稳态、无内热源
即数学上的拉普拉斯方程。
⑤一维，常物性，稳态，无内热源 
即： 
2 ）圆柱坐标系中的导热微分方程
= 
3 ）球坐标系中的导热微分方程
= 
综上说明：
（ 1 ）导热问题仍然服从能量守恒定律；
（ 2 ）等号左边是单位时间内微元体热力学能的增量（非稳态项）；
（ 3 ）等号右边前三项之和是通过界面的导热使微分元体在单位时间内增加的能量 ( 扩散项 ) ；
（ 4 ）等号右边最后项是源项；
（ 5 ）若某坐标方向上温度不变，该方向的净导热量为零，则相应的扩散项即从导热微分方程中消失。
通过导热微分方程可知，求解导热问题，实际上就是对导热微分方程式的求解。预知某一导热问题的温度分布，必须给出表征该问题的附加条件。
二、 定解条件
1 、定义：指使导热微分方程获得适合某一特定导热问题的求解的附加条件。
2 、分类：1 ）初始条件：初始时间温度分布的初始条件；
2 ）边界条件：导热物体边界上温度或换热情况的边界条件。
说明： ①非稳态导热定解条件有两个；
②稳态导热定解条件只有边界条件，无初始条件。
3 、导热问题的常见边界条件可归纳为以下三类
1 ）规定了边界上的温度值，称第一类边界条件 , 即 t w =C 。对于非稳态导热这类边界条件要求给出以下关系，τ >0 时 ,tw =f1 ( τ ) ；
2 ）规定了边界上的热流密度值 , 称为第二类边界条件；
对于非稳态导热这类边界条件要求给出以下关系式：
当τ >0 时， 
式中 n ——为表面 A 的法线方向
3 ）规定了边界上物体与周围流体间的表面传热系数 h 以及周围流体的温度 
，称为第三类边界条件。
以物体被冷却为例： 
对于非稳态导热，式中 h 、 均是τ的函数。
三、有关说明
1 、热扩散率的物理意义
由热扩散率的定义：
可知：
1 ） 
是物体的导热系数， 
越大，在相同温度梯度下，可以传导更多的热量。
2) 
是单位体积的物体温度升高 1 ℃所需的热量。 越小，温度升高 1 ℃所吸收的热量越少，可以剩下更多的热量向物体内部传递，使物体内温度更快的随界面温度升高而升高。由此可见a物理意义：
① ɑ越大，表示物体受热时，其内部各点温度扯平的能力越大。
② ɑ越大，表示物体中温度变化传播的越快。所以，ɑ也是材料传播温度变化能力大小的指标，亦称导温系数。
2 、导热微分方程的适用范围
1 ）适用于 q 不很高，而作用时间长。同时傅立叶定律也适用该条件。
2 ）若时间极短，而且热流密度极大时，则不适用。
3 ）若属极低温度（ -273 ℃）时的导热不适用。
